Article status: Draft
Time Estimate for Reading: 30 min
Learning Objectives: Summarizing the concept of Power
Effort Required: Medium
Pedagogy Model: Evolution, Formula Analysis, Inter-disciplinary
Prior Physics Concepts: displacement, velocity, acceleration, mass, power, force
Prior Math Tools: Secondary school level Arithmetic, geometry and algebra
We have been discussing about power of motion and power of rest without considering how do we provide this power. providing power would require an interaction. May be we can visualize power applied as discrete (per second) impacts. For an interaction it takes some amount of displacement and time. But before we get into impacts, we need to understand a little more of rest. Even rest is a result of invisible discrete impacts. we call it continuous push but in reality, they are discrete.
Let us continue with "rest". We discussed about falling bodies and got to understand that independent of mass, all of them fall with constant acceleration. we seem to repeat this quiet often. This seems to be the starting point for every thing. Starting with this we were able to define and measure mass. we were able to measure constant velocity and constant acceleration motion. we also deduced the concept of force and ended up with equal and opposite reactions.
So, we will be looking at two situations. one, a ball at rest on a table. Second, how do we keep a ping-pong ball at rest without a table.
Situation 1- Ball on table:
Let us resume our discussion from "power of rest". An object should not accelerate and we need to provide an acceleration in the opposite direction. This can be provided by placing the ball on a reasonably rigid table; table providing the necessary opposite acceleration.
So, the invisible springs in the table will be acting on the ball continuously. the word continuously is important here (you may refer to "power of motion" as a refresher). We may visualize it like this. The table, seeming at rest, pushes (accelerates) the ball, a very little, upward, for a very short duration and comes back to its initial position. the ball falls down along with the table. this process goes on again and again. this may not be visible to our eye but this is what must be happening (based on our understanding so far). You might have come across sagging rack's. racks's left unattended for a long period, might sag due it's self weight. There is fatigue. Even inanimate objects seems to get tired.
You might have experienced this if have tried to retain a trolley at rest in an inclined plane. you could feel the trolley pushing (or pulling) back on you. this would not be the case if you left the trolley on a horizontal plane. there is no motion. that is no visible acceleration or deceleration of the trolley. How do we handle this?
With advancement in science, we came to know that atoms and molecules are in continuous motion. A measure of this motion is termed as heat energy (total kinetic energy of all molecules. but the concept of kinetic energy is yet to be discovered). So, power for acceleration might be taken from the atmosphere. Image something like this. The table pushes on the ball and loses some power and there would be a drop in temperature (average kinetic energy of molecules). It is natural for all bodies to be at the same temperature. So, atmosphere provides this to the table. So, looks like every object, seeming at rest is an engine working at microscopic level.
We are still in the days of newton. atomic structure, engines, understanding of heat and temperature and yet to be discovered.
So, newton might have come to a conclusion that, for objects at rest, we do not require any power. All that we need is an acceleration in the opposite direction. Some how, the earth along with the table should provide this acceleration. Action = reaction again.
Situation 2: Ping-pong ball at rest without table
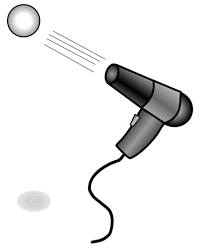
The concept of rest can be better understood if we try to balance a ping-pong ball by blowing air with the help of a compressor driven by electric motor (instead of seeking support from earth by resting it on a table). With out getting into the actual numbers, this is how it works. The pin-pong ball has some mass 'm'. it is naturally accelerated towards the earth by a quantity 'g'. for this ball to remain at rest we need to provide an acceleration opposite to 'g'. How can air that we blow offer this equal acceleration?
We know how to calculate the power required for uniform velocity motion.
power = mass of ball * acceleration x uniform velocity
This power should be provided by electric motor and is equal to V*I (more on this later)
Motor should give this power to air. So for air,
Acceleration required should be equal to 'g'. equal and opposite reactions.
the mass of air displaced should be equal to mass of ping-pong ball. mass of air can be calculated from the volume of ball . for the sake of simplicity, consider the ball to be a cylinder of diameter d and height h. knowing the density of air, we can calculate the mass of air that will occupy the volume of 1 ball. from this information, we can calculate the can calculate the height of the cylinder required for an equal amount of air.
This height of air has to be displaced in 1 sec. that brings us to calculate the velocity.
Now power of air = mass of air * acceleration of air * velocity.
Since this air passes over the ball, the velocity of air will not carry the ball away and it will just keep the ball at rest. The concept of continuous interaction.
So, the power of motor should can be calculated by an appropriate choice of voltage and current.
There are some factors which we have not considered, but this would gives us an understanding that it takes some power to keep an object at rest. another example would be the hill start feature in automobiles.
We just used a simple method. There are other accurate methods using Bernoulli's principle which were discovered later.
Even rest requires power.
Having discussed on rest, we can move on to deformation and Impact.
What happens to objects when they hit the ground after a free fall? A solid ball does not break nor bounce back, a rubber ball bounces back to more or less the same height, an egg or tomato loses its shape beyond recognition.
When an egg hits the ground, we call this Interaction an impact, egg undergoes deformation. The atoms and molecules that form the shell of the egg can only undergo a certain amount of deformation and beyond this they will break. A macroscopic study has a relationship between stress and strain. Within a specific limit of strain, the objects would not break or yield. We have introduced a few words like stress and strain to our vocabulary. To understand these words, we need to add one more word pressure, which we shall take it up later.
Objects that bounce back are considered to be elastic. They can deform without breaking.
We can summarize the discussions as follows.
- For an object to be at rest we use m1a1 = m2a2 (supported by table or earth)
- For an object to be at rest without support from earth we need power (ping-pong ball example).
- When applying power, one object (cause) interacts with another object (effect) and during an interaction, there would be deformations at macroscopic and microscopic level
- If either object does not withstand this deformation, objects may break and we would not get the intended motion
In the discussions on power of motion we had the engine and object moving together. The engine providing the necessary power for the object to move with a required velocity or acceleration.
 In the discussions on power of rest of ping-pong ball we had air moving past the ball.
In the discussions on power of rest of ping-pong ball we had air moving past the ball.
But in applications like bat hitting a ball (gun firing a bullet, bow and arrow etc), the bat does not travel along with the ball. We shall get into the regime of special class of interactions called "collisions" in the next article.
Time Estimate for Reading: 30 min
Learning Objectives: Summarizing the concept of Power
Effort Required: Medium
Pedagogy Model: Evolution, Formula Analysis, Inter-disciplinary
Prior Physics Concepts: displacement, velocity, acceleration, mass, power, force
Prior Math Tools: Secondary school level Arithmetic, geometry and algebra
Let us continue with "rest". We discussed about falling bodies and got to understand that independent of mass, all of them fall with constant acceleration. we seem to repeat this quiet often. This seems to be the starting point for every thing. Starting with this we were able to define and measure mass. we were able to measure constant velocity and constant acceleration motion. we also deduced the concept of force and ended up with equal and opposite reactions.
So, we will be looking at two situations. one, a ball at rest on a table. Second, how do we keep a ping-pong ball at rest without a table.
Situation 1- Ball on table:
Let us resume our discussion from "power of rest". An object should not accelerate and we need to provide an acceleration in the opposite direction. This can be provided by placing the ball on a reasonably rigid table; table providing the necessary opposite acceleration.
Notice the use of word reasonably rigid. If the table is not rigid enough, it would undergo extensive deformation (imagine placing this ball on a cloth) and in extreme cases, it might even break.
This brings us to another question. How can a non-moving table provide acceleration in the opposite direction? To answer this question, let us consider a simple example of pressing a ball with our fingers. Once we release our fingers, the ball gets back to its original shape. We can roughly imagine the ball to be made of springs inside (relate it to the newtons mass determination experiment). So springs when released, have the ability to provide an acceleration. The amount of push (or acceleration) the spring can provide is given as kx. K is the stiffness of the spring and x representing the displacement. A wooden table in this case acts like a spring (the deformation will be so minuscule and may not be visible to the naked eye).
The concept of spring may be used as a means of visualization. Later in the 18th century, once we understood that matter is made of atoms and atoms in turn are made of charged particles, the effect of spring comes from repulsion between electric charges. The invisible springs.
So, the invisible springs in the table will be acting on the ball continuously. the word continuously is important here (you may refer to "power of motion" as a refresher). We may visualize it like this. The table, seeming at rest, pushes (accelerates) the ball, a very little, upward, for a very short duration and comes back to its initial position. the ball falls down along with the table. this process goes on again and again. this may not be visible to our eye but this is what must be happening (based on our understanding so far). You might have come across sagging rack's. racks's left unattended for a long period, might sag due it's self weight. There is fatigue. Even inanimate objects seems to get tired.
You might have experienced this if have tried to retain a trolley at rest in an inclined plane. you could feel the trolley pushing (or pulling) back on you. this would not be the case if you left the trolley on a horizontal plane. there is no motion. that is no visible acceleration or deceleration of the trolley. How do we handle this?
With advancement in science, we came to know that atoms and molecules are in continuous motion. A measure of this motion is termed as heat energy (total kinetic energy of all molecules. but the concept of kinetic energy is yet to be discovered). So, power for acceleration might be taken from the atmosphere. Image something like this. The table pushes on the ball and loses some power and there would be a drop in temperature (average kinetic energy of molecules). It is natural for all bodies to be at the same temperature. So, atmosphere provides this to the table. So, looks like every object, seeming at rest is an engine working at microscopic level.
We are still in the days of newton. atomic structure, engines, understanding of heat and temperature and yet to be discovered.
So, newton might have come to a conclusion that, for objects at rest, we do not require any power. All that we need is an acceleration in the opposite direction. Some how, the earth along with the table should provide this acceleration. Action = reaction again.
Situation 2: Ping-pong ball at rest without table
The concept of rest can be better understood if we try to balance a ping-pong ball by blowing air with the help of a compressor driven by electric motor (instead of seeking support from earth by resting it on a table). With out getting into the actual numbers, this is how it works. The pin-pong ball has some mass 'm'. it is naturally accelerated towards the earth by a quantity 'g'. for this ball to remain at rest we need to provide an acceleration opposite to 'g'. How can air that we blow offer this equal acceleration?
We know how to calculate the power required for uniform velocity motion.
power = mass of ball * acceleration x uniform velocity
This power should be provided by electric motor and is equal to V*I (more on this later)
Motor should give this power to air. So for air,
Acceleration required should be equal to 'g'. equal and opposite reactions.
the mass of air displaced should be equal to mass of ping-pong ball. mass of air can be calculated from the volume of ball . for the sake of simplicity, consider the ball to be a cylinder of diameter d and height h. knowing the density of air, we can calculate the mass of air that will occupy the volume of 1 ball. from this information, we can calculate the can calculate the height of the cylinder required for an equal amount of air.
This height of air has to be displaced in 1 sec. that brings us to calculate the velocity.
Now power of air = mass of air * acceleration of air * velocity.
Since this air passes over the ball, the velocity of air will not carry the ball away and it will just keep the ball at rest. The concept of continuous interaction.
So, the power of motor should can be calculated by an appropriate choice of voltage and current.
There are some factors which we have not considered, but this would gives us an understanding that it takes some power to keep an object at rest. another example would be the hill start feature in automobiles.
We just used a simple method. There are other accurate methods using Bernoulli's principle which were discovered later.
Even rest requires power.
Having discussed on rest, we can move on to deformation and Impact.
What happens to objects when they hit the ground after a free fall? A solid ball does not break nor bounce back, a rubber ball bounces back to more or less the same height, an egg or tomato loses its shape beyond recognition.
When an egg hits the ground, we call this Interaction an impact, egg undergoes deformation. The atoms and molecules that form the shell of the egg can only undergo a certain amount of deformation and beyond this they will break. A macroscopic study has a relationship between stress and strain. Within a specific limit of strain, the objects would not break or yield. We have introduced a few words like stress and strain to our vocabulary. To understand these words, we need to add one more word pressure, which we shall take it up later.
Objects that bounce back are considered to be elastic. They can deform without breaking.
We can summarize the discussions as follows.
- For an object to be at rest we use m1a1 = m2a2 (supported by table or earth)
- For an object to be at rest without support from earth we need power (ping-pong ball example).
- When applying power, one object (cause) interacts with another object (effect) and during an interaction, there would be deformations at macroscopic and microscopic level
- If either object does not withstand this deformation, objects may break and we would not get the intended motion
In the discussions on power of motion we had the engine and object moving together. The engine providing the necessary power for the object to move with a required velocity or acceleration.
But in applications like bat hitting a ball (gun firing a bullet, bow and arrow etc), the bat does not travel along with the ball. We shall get into the regime of special class of interactions called "collisions" in the next article.